Determine the Limit of Each of the Following Bc Calculus Review 1-1
2. Limits
2.2 The Limit of a Role
Learning Objectives
- Using correct annotation, depict the limit of a part.
- Use a tabular array of values to estimate the limit of a office or to identify when the limit does not exist.
- Utilise a graph to gauge the limit of a function or to identify when the limit does not exist.
- Ascertain one-sided limits and provide examples.
- Explain the relationship between one-sided and ii-sided limits.
- Using right notation, describe an infinite limit.
- Define a vertical asymptote.
The concept of a limit or limiting procedure, essential to the understanding of calculus, has been around for thousands of years. In fact, early mathematicians used a limiting process to obtain ameliorate and ameliorate approximations of areas of circles. Yet, the formal definition of a limit—equally we know and empathize it today—did not appear until the late 19th century. We therefore begin our quest to understand limits, equally our mathematical ancestors did, past using an intuitive arroyo. At the end of this chapter, armed with a conceptual understanding of limits, we examine the formal definition of a limit.
We begin our exploration of limits by taking a look at the graphs of the functions
![]() , and
, and ![]() ,
,
which are shown in (Figure). In particular, allow'due south focus our attention on the behavior of each graph at and around ![]() .
.
Each of the three functions is undefined at ![]() , but if we make this statement and no other, we requite a very incomplete movie of how each office behaves in the vicinity of
, but if we make this statement and no other, we requite a very incomplete movie of how each office behaves in the vicinity of ![]() . To limited the behavior of each graph in the vicinity of ii more completely, nosotros demand to innovate the concept of a limit.
. To limited the behavior of each graph in the vicinity of ii more completely, nosotros demand to innovate the concept of a limit.
Intuitive Definition of a Limit
Permit'due south commencement have a closer look at how the function ![]() behaves around
behaves around ![]() in (Figure). As the values of
in (Figure). As the values of ![]() approach 2 from either side of ii, the values of
approach 2 from either side of ii, the values of ![]() arroyo four. Mathematically, we say that the limit of
arroyo four. Mathematically, we say that the limit of ![]() as
as ![]() approaches 2 is 4. Symbolically, we express this limit as
approaches 2 is 4. Symbolically, we express this limit as
![]() .
.
From this very brief informal wait at i limit, let'southward commencement to develop an intuitive definition of the limit. We tin can call back of the limit of a office at a number ![]() as existence the one real number
as existence the one real number ![]() that the functional values approach as the
that the functional values approach as the ![]() -values approach
-values approach ![]() , provided such a real number
, provided such a real number ![]() exists. Stated more carefully, nosotros have the following definition:
exists. Stated more carefully, nosotros have the following definition:
We can approximate limits by constructing tables of functional values and by looking at their graphs. This process is described in the following Problem-Solving Strategy.
Problem-Solving Strategy: Evaluating a Limit Using a Table of Functional Values
- To evaluate
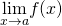 , we begin past completing a table of functional values. We should cull ii sets of
, we begin past completing a table of functional values. We should cull ii sets of 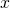 -values—ane ready of values budgeted
-values—ane ready of values budgeted  and less than
and less than  , and another set of values approaching
, and another set of values approaching  and greater than
and greater than  . (Effigy) demonstrates what your tables might look like.
. (Effigy) demonstrates what your tables might look like.
Table of Functional Values for 
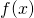
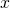
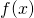
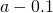
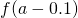
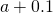
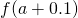
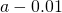
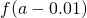
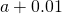
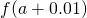
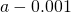
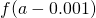
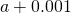
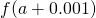
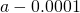
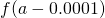
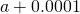
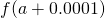
Use boosted values as necessary. Use additional values every bit necessary. - Next, let's await at the values in each of the
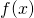 columns and decide whether the values seem to be approaching a single value every bit we move downwards each column. In our columns, nosotros await at the sequence
columns and decide whether the values seem to be approaching a single value every bit we move downwards each column. In our columns, nosotros await at the sequence 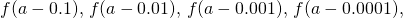 and and then on, and
and and then on, and 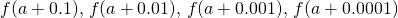 and so on. (Note: Although we have chosen the
and so on. (Note: Although we have chosen the 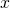 -values
-values 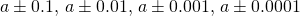 , then along, and these values will probably work well-nigh every time, on very rare occasions we may need to modify our choices.)
, then along, and these values will probably work well-nigh every time, on very rare occasions we may need to modify our choices.) - If both columns approach a common
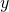 -value
-value 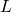 , we state
, we state 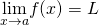 . We tin can use the following strategy to ostend the effect obtained from the table or equally an alternative method for estimating a limit.
. We tin can use the following strategy to ostend the effect obtained from the table or equally an alternative method for estimating a limit. - Using a graphing estimator or estimator software that allows us graph functions, we can plot the office
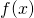 , making sure the functional values of
, making sure the functional values of 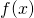 for
for 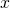 -values near
-values near  are in our window. Nosotros can apply the trace characteristic to motility along the graph of the function and watch the
are in our window. Nosotros can apply the trace characteristic to motility along the graph of the function and watch the 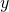 -value readout equally the
-value readout equally the 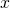 -values approach
-values approach  . If the
. If the 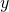 -values approach
-values approach 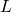 as our
as our 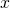 -values arroyo
-values arroyo  from both directions, then
from both directions, then 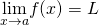 . Nosotros may need to zoom in on our graph and repeat this procedure several times.
. Nosotros may need to zoom in on our graph and repeat this procedure several times.
We utilize this Problem-Solving Strategy to compute a limit in (Figure).
Evaluating a Limit Using a Tabular array of Functional Values ane
Evaluate ![]() using a tabular array of functional values.
using a tabular array of functional values.
Evaluating a Limit Using a Tabular array of Functional Values two
Evaluate ![]() using a table of functional values.
using a table of functional values.
Estimate ![]() using a tabular array of functional values. Use a graph to confirm your gauge.
using a tabular array of functional values. Use a graph to confirm your gauge.
Solution
![]()
At this point, nosotros encounter from (Figure) and (Effigy) that it may exist but as piece of cake, if not easier, to gauge a limit of a function past inspecting its graph as information technology is to estimate the limit by using a tabular array of functional values. In (Figure), we evaluate a limit exclusively by looking at a graph rather than by using a table of functional values.
Evaluating a Limit Using a Graph
For ![]() shown in (Figure), evaluate
shown in (Figure), evaluate ![]() .
.
Based on (Figure), we make the following observation: It is possible for the limit of a function to exist at a point, and for the function to be defined at this indicate, but the limit of the function and the value of the part at the betoken may be different.
Use the graph of ![]() in (Effigy) to evaluate
in (Effigy) to evaluate ![]() , if possible.
, if possible.
Solution
![]() .
.
Looking at a table of functional values or looking at the graph of a function provides united states of america with useful insight into the value of the limit of a office at a given point. However, these techniques rely likewise much on guesswork. Nosotros eventually need to develop culling methods of evaluating limits. These new methods are more algebraic in nature and we explore them in the next section; nevertheless, at this point we introduce two special limits that are foundational to the techniques to come.
Two Important Limits
Let ![]() be a real number and
be a real number and ![]() be a constant.
be a constant.
We can brand the following observations about these 2 limits.
- For the first limit, observe that every bit
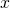 approaches
approaches  , so does
, so does 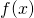 , because
, because 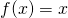 . Consequently,
. Consequently, 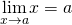 .
. - For the 2d limit, consider (Figure).
| | | | | |
|---|---|---|---|---|
| | | | | |
| | | | | |
| | | | | |
| | | | |
Observe that for all values of ![]() (regardless of whether they are approaching
(regardless of whether they are approaching ![]() ), the values
), the values ![]() remain constant at
remain constant at ![]() . Nosotros accept no selection but to conclude
. Nosotros accept no selection but to conclude ![]() .
.
The Existence of a Limit
Equally nosotros consider the limit in the side by side instance, go on in mind that for the limit of a part to exist at a signal, the functional values must approach a unmarried real-number value at that point. If the functional values do not approach a single value, then the limit does non exist.
Evaluating a Limit That Fails to Be
Evaluate ![]() using a table of values.
using a table of values.
Employ a table of functional values to evaluate ![]() , if possible.
, if possible.
Solution
![]() does not exist.
does not exist.
One-Sided Limits
Sometimes indicating that the limit of a function fails to be at a point does not provide united states of america with plenty data nigh the behavior of the function at that particular signal. To see this, we now revisit the function ![]() introduced at the beginning of the section (run into (Effigy)(b)). Equally nosotros option values of
introduced at the beginning of the section (run into (Effigy)(b)). Equally nosotros option values of ![]() close to 2,
close to 2, ![]() does not approach a single value, so the limit as
does not approach a single value, so the limit as ![]() approaches 2 does not exist—that is,
approaches 2 does not exist—that is, ![]() DNE. However, this argument alone does not give u.s. a complete motion picture of the beliefs of the function around the
DNE. However, this argument alone does not give u.s. a complete motion picture of the beliefs of the function around the ![]() -value 2. To provide a more than authentic clarification, we introduce the idea of a one-sided limit. For all values to the left of ii (or the negative side of 2),
-value 2. To provide a more than authentic clarification, we introduce the idea of a one-sided limit. For all values to the left of ii (or the negative side of 2), ![]() . Thus, as
. Thus, as ![]() approaches 2 from the left,
approaches 2 from the left, ![]() approaches −i. Mathematically, we say that the limit as
approaches −i. Mathematically, we say that the limit as ![]() approaches two from the left is −1. Symbolically, we express this idea equally
approaches two from the left is −1. Symbolically, we express this idea equally
![]() .
.
Similarly, as ![]() approaches 2 from the right (or from the positive side),
approaches 2 from the right (or from the positive side), ![]() approaches 1. Symbolically, we express this thought as
approaches 1. Symbolically, we express this thought as
![]() .
.
We tin now present an breezy definition of one-sided limits.
Evaluating 1-Sided Limits
Employ a table of functional values to judge the following limits, if possible.
Solution
a. ![]() ; b.
; b. ![]()
Let u.s. at present consider the relationship between the limit of a function at a signal and the limits from the right and left at that indicate. It seems clear that if the limit from the right and the limit from the left have a common value, then that common value is the limit of the function at that bespeak. Similarly, if the limit from the left and the limit from the correct take on unlike values, the limit of the role does not be. These conclusions are summarized in (Effigy).
Infinite Limits
Evaluating the limit of a function at a point or evaluating the limit of a part from the right and left at a point helps the states to characterize the behavior of a function around a given value. As we shall meet, we tin can also describe the behavior of functions that do not have finite limits.
We now plough our attention to ![]() , the third and final function introduced at the outset of this section (see (Figure)(c)). From its graph we run into that equally the values of
, the third and final function introduced at the outset of this section (see (Figure)(c)). From its graph we run into that equally the values of ![]() approach 2, the values of
approach 2, the values of ![]() become larger and larger and, in fact, become infinite. Mathematically, we say that the limit of
become larger and larger and, in fact, become infinite. Mathematically, we say that the limit of ![]() equally
equally ![]() approaches 2 is positive infinity. Symbolically, we express this thought equally
approaches 2 is positive infinity. Symbolically, we express this thought equally
![]() .
.
More by and large, nosotros define space limits as follows:
It is important to sympathise that when we write statements such every bit ![]() or
or ![]() we are describing the behavior of the function, every bit we have just defined information technology. Nosotros are not asserting that a limit exists. For the limit of a function
we are describing the behavior of the function, every bit we have just defined information technology. Nosotros are not asserting that a limit exists. For the limit of a function ![]() to be at
to be at ![]() , it must arroyo a real number
, it must arroyo a real number ![]() every bit
every bit ![]() approaches
approaches ![]() . That said, if, for case,
. That said, if, for case, ![]() , we ever write
, we ever write ![]() rather than
rather than ![]() DNE.
DNE.
Recognizing an Space Limit
It is useful to point out that functions of the form ![]() , where
, where ![]() is a positive integer, have infinite limits equally
is a positive integer, have infinite limits equally ![]() approaches
approaches ![]() from either the left or right ((Figure)). These limits are summarized in (Figure).
from either the left or right ((Figure)). These limits are summarized in (Figure).
Infinite Limits from Positive Integers
If ![]() is a positive even integer, and then
is a positive even integer, and then
![]() .
.
If ![]() is a positive odd integer, then
is a positive odd integer, then
![]()
and
![]() .
.
We should as well signal out that in the graphs of ![]() , points on the graph having
, points on the graph having ![]() -coordinates very most to
-coordinates very most to ![]() are very close to the vertical line
are very close to the vertical line ![]() . That is, as
. That is, as ![]() approaches
approaches ![]() , the points on the graph of
, the points on the graph of ![]() are closer to the line
are closer to the line ![]() . The line
. The line ![]() is chosen a vertical asymptote of the graph. We formally define a vertical asymptote every bit follows:
is chosen a vertical asymptote of the graph. We formally define a vertical asymptote every bit follows:
Definition
Allow ![]() exist a office. If any of the following weather condition hold, then the line
exist a office. If any of the following weather condition hold, then the line ![]() is a vertical asymptote of
is a vertical asymptote of ![]() :
:
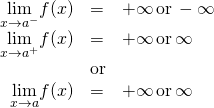
Finding a Vertical Asymptote
Solution
a. ![]() ;
;
b. ![]() ;
;
c. ![]() DNE. The line
DNE. The line ![]() is the vertical asymptote of
is the vertical asymptote of ![]() .
.
In the next case we put our knowledge of various types of limits to utilize to clarify the behavior of a function at several different points.
Behavior of a Function at Different Points
Chapter Opener: Einstein's Equation

In the chapter opener we mentioned briefly how Albert Einstein showed that a limit exists to how fast any object can travel. Given Einstein'due south equation for the mass of a moving object, what is the value of this leap?
Solution
Our starting point is Einstein'due south equation for the mass of a moving object,
![]() ,
,
where ![]() is the object'south mass at rest,
is the object'south mass at rest, ![]() is its speed, and
is its speed, and ![]() is the speed of lite. To see how the mass changes at high speeds, we can graph the ratio of masses
is the speed of lite. To see how the mass changes at high speeds, we can graph the ratio of masses ![]() every bit a function of the ratio of speeds,
every bit a function of the ratio of speeds, ![]() ((Figure)).
((Figure)).
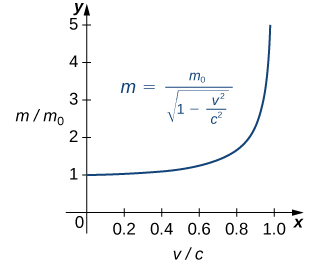
We tin can come across that as the ratio of speeds approaches ane—that is, as the speed of the object approaches the speed of light—the ratio of masses increases without bound. In other words, the function has a vertical asymptote at ![]() . We tin can try a few values of this ratio to examination this idea.
. We tin can try a few values of this ratio to examination this idea.
| | | |
|---|---|---|
| 0.99 | 0.1411 | 7.089 |
| 0.999 | 0.0447 | 22.37 |
| 0.9999 | 0.0141 | seventy.71 |
Thus, according to (Figure), if an object with mass 100 kg is traveling at 0.9999![]() , its mass becomes 7071 kg. Since no object can have an infinite mass, we conclude that no object can travel at or more than the speed of light.
, its mass becomes 7071 kg. Since no object can have an infinite mass, we conclude that no object can travel at or more than the speed of light.
Key Concepts
- A tabular array of values or graph may be used to estimate a limit.
- If the limit of a function at a signal does not exist, it is still possible that the limits from the left and right at that point may exist.
- If the limits of a part from the left and right exist and are equal, then the limit of the function is that common value.
- We may utilise limits to depict space beliefs of a role at a indicate.
Fundamental Equations
For the following exercises, consider the function ![]() .
.
2.What do your results in the preceding exercise indicate near the two-sided limit ![]() ? Explain your response.
? Explain your response.
Solution
![]() does not exist because
does not exist because ![]() .
.
For the following exercises, consider the function ![]() .
.
four.What does the tabular array of values in the preceding do betoken virtually the function ![]() ?
?
Solution
![]()
5.To which mathematical constant does the limit in the preceding exercise appear to be getting closer?
In the post-obit exercises, use the given values of ![]() to prepare a tabular array to evaluate the limits. Round your solutions to eight decimal places.
to prepare a tabular array to evaluate the limits. Round your solutions to eight decimal places.
Solution
a. i.98669331; b. 1.99986667; c. 1.99999867; d. 1.99999999; e. 1.98669331; f. 1.99986667; g. 1.99999867; h. 1.99999999; ![]()
8.Use the preceding two exercises to conjecture (guess) the value of the following limit: ![]() for
for ![]() , a positive existent value.
, a positive existent value.
Solution
![]()
In the following exercises, set up up a table of values to find the indicated limit. Round to eight digits.
Solution
a. −0.80000000; b. −0.98000000; c. −0.99800000; d. −0.99980000; east. −i.2000000; f. −one.0200000; thou. −1.0020000; h. −1.0002000;
![]()
Solution
a. −37.931934; b. −3377.9264; c. −333,777.93; d. −33,337,778; eastward. −29.032258; f. −3289.0365; g. −332,889.04; h. −33,328,889
![]()
Solution
a. 0.13495277; b. 0.12594300; c. 0.12509381; d. 0.12500938; e. 0.11614402; f. 0.12406794; k. 0.12490631; h. 0.12499063;
![]()
In the following exercises, gear up up a table of values and round to viii pregnant digits. Based on the table of values, brand a guess near what the limit is. And then, employ a calculator to graph the office and determine the limit. Was the conjecture right? If not, why does the method of tables fail?
Solution
a. −x.00000; b. −100.00000; c. −1000.0000; d. −10,000.000; Guess: ![]() , Actual: DNE
, Actual: DNE
![A graph of the function (1/alpha) * cos (pi / alpha), which oscillates gently until the interval [-.2, .2], where it oscillates rapidly, going to infinity and negative infinity as it approaches the y axis.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11202929/CNX_Calc_Figure_02_02_214.jpg)
In the post-obit exercises, consider the graph of the function ![]() shown here. Which of the statements most
shown here. Which of the statements most ![]() are true and which are faux? Explain why a argument is imitation.
are true and which are faux? Explain why a argument is imitation.
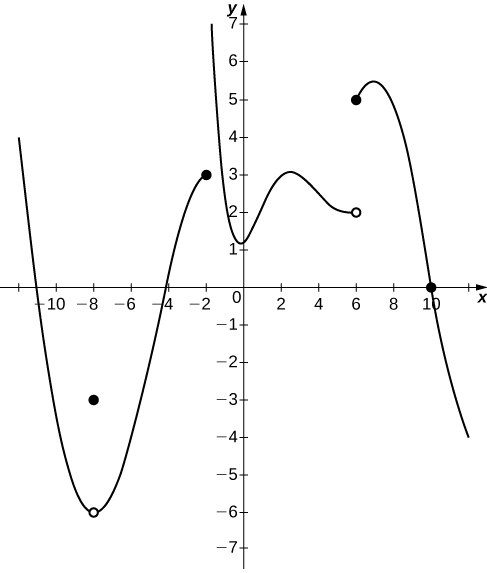
17. ![]()
18. ![]()
Solution
False; ![]()
nineteen. ![]()
xx. ![]()
In the following exercises, use the following graph of the function ![]() to notice the values, if possible. Estimate when necessary.
to notice the values, if possible. Estimate when necessary.
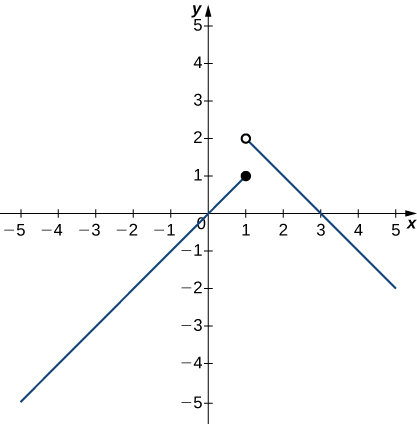 one. The offset segment is linear with a slope of 1 and goes through the origin. Its endpoint is a closed circle at (1,1). The 2nd segment is also linear with a slope of -ane. It begins with the open circle at (i,two).">
one. The offset segment is linear with a slope of 1 and goes through the origin. Its endpoint is a closed circle at (1,1). The 2nd segment is also linear with a slope of -ane. It begins with the open circle at (i,two).">
21. ![]()
22. ![]()
23. ![]()
24. ![]()
25. ![]()
In the following exercises, utilize the graph of the part ![]() shown here to find the values, if possible. Approximate when necessary.
shown here to find the values, if possible. Approximate when necessary.
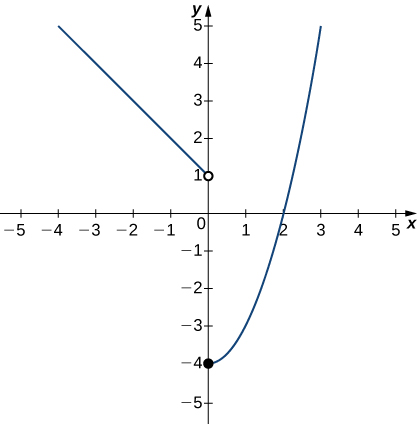
26. ![]()
27. ![]()
28. ![]()
29. ![]()
In the following exercises, apply the graph of the function ![]() shown here to observe the values, if possible. Estimate when necessary.
shown here to observe the values, if possible. Estimate when necessary.
 2, has a gradient of 1, and begins at the open circle (2,2).">
2, has a gradient of 1, and begins at the open circle (2,2).">
30. ![]()
31. ![]()
32. ![]()
33. ![]()
34. ![]()
35. ![]()
In the following exercises, use the graph of the function ![]() shown hither to find the values, if possible. Estimate when necessary.
shown hither to find the values, if possible. Estimate when necessary.
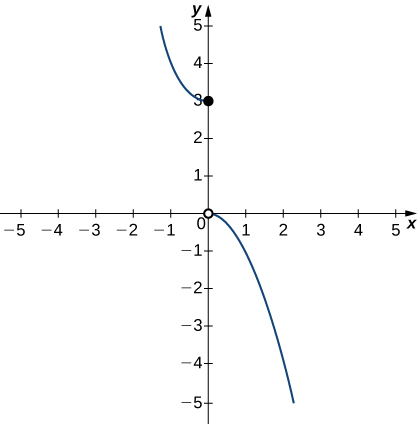 =0 and is the left one-half of an upward opening parabola with vertex at the closed circle (0,iii). The second exists for x>0 and is the right one-half of a downwards opening parabola with vertex at the open circle (0,0).">
=0 and is the left one-half of an upward opening parabola with vertex at the closed circle (0,iii). The second exists for x>0 and is the right one-half of a downwards opening parabola with vertex at the open circle (0,0).">
36. ![]()
37. ![]()
38. ![]()
In the post-obit exercises, use the graph of the role ![]() shown hither to find the values, if possible. Estimate when necessary.
shown hither to find the values, if possible. Estimate when necessary.
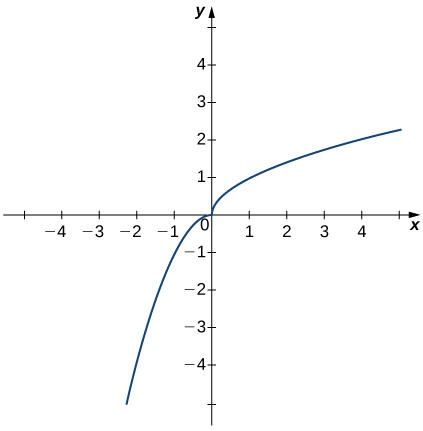
39. ![]()
xl. ![]()
41. ![]()
In the following exercises, employ the graph of the part ![]() shown hither to find the values, if possible. Gauge when necessary.
shown hither to find the values, if possible. Gauge when necessary.
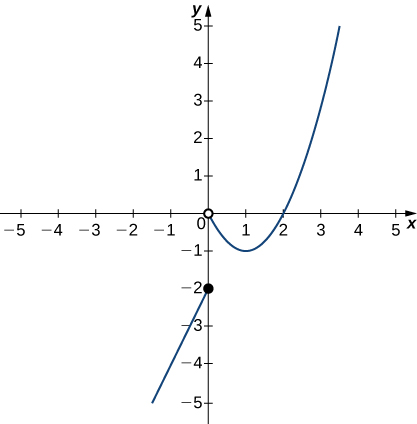 0, and in that location is a airtight circumvolve at the origin.">
0, and in that location is a airtight circumvolve at the origin.">
42. ![]()
43. ![]()
44. ![]()
45. ![]()
46. ![]()
In the following exercises, sketch the graph of a part with the given properties.
47. ![]() , the function is non divers at
, the function is non divers at ![]() .
.
48. ![]() ,
, ![]()
Solution
Answers may vary.
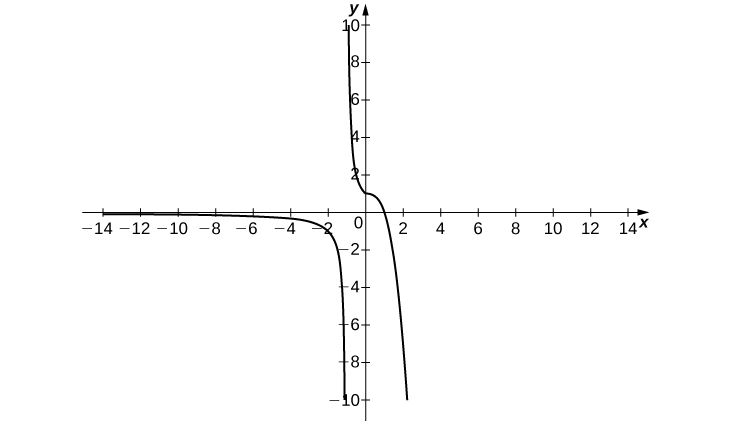
49. ![]() ,
, ![]()
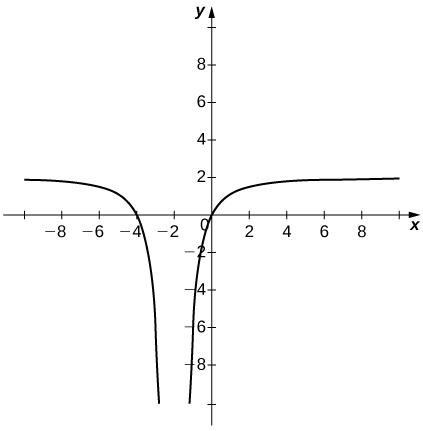
50. ![]() ,
,![]()
Solution
Answers may vary.
51. 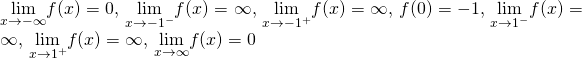
Source: https://opentextbc.ca/calculusv1openstax/chapter/the-limit-of-a-function/